
Innehåll
- Zipfs lag förklarade
- Grundläggande experiment
- Zipfs lag på ångmarknaderna
- Vad kan vi lära oss om Steam?
- Slutsatser
För en kort tid sedan föreslog en vän att jag tittade på Vsauces-video på Zipfs lag, Paretos princip och deras mystiska utseenden runt omkring oss. Här är en liten teaser för att uppmärksamma dig - 80% av alla bor i 20% av de mest populära städerna. 80% av allt mark tillhör 20% av de rikaste hyresvärdarna 80% av allt papperskorgen ligger på de 20% tråkigaste gatorna - som förutses av Zipfs lag och Paretos princip.
Inte tillräckligt? Tja, som jag upptäckte igår, slutar kaninhålet inte där ... Full av skepticism, bestämde jag mig för att titta på hur mycket tid folk spenderar att spela Steam-spel ... Tja. 80% av människornas tid spenderas att spela 20% av de populäraste spelen ... Intressant? Tja, läs vidare, det finns mer till den här historien.
Klocka in på över 20min, Vsauces strävan är fantastisk och förklarar mycket av de stora bilden saker om Zipf, men han är väldigt blyg för att visa oss kärnan mekanismen som är allmänt trodde att bidra till varför Zipf fungerar hur det gör. Så innan vi fortsätter vill jag kortfattat förklara det.
Zipfs lag förklarade
Det finns flera begreppsmässiga sätt att förklara intuitionen bakom 20/80-principen. Det bästa exemplet är enligt min mening en fråga om Moon craters.
Grundläggande experiment
Så, tänk om du vill, att det finns en orörd mån - en perfekt slät yta. Nu, säg att det finns några slumpmässigt dimensionerade asteroider som slår Månen iväg. När den första asteroiden landar, lämnar den en krater. Nu träffar en annan, lämnar en krater någon annanstans. Varje krater är en del av den totala ytan, därför finns det en chans att nästa slumpmässiga asteroid kommer att slå nära en befintlig krater och gå med i den, bilda en grupp. Chansen att en ny asteroid som träffar en given krater är då proportionell mot kraters och asteroidernas existerande storlek. Det betyder att nästa slumpmässiga asteroid är mer benägna att gå med i den största befintliga gruppen, vilket gör den ännu större. En slags kumulativ process, som då skapar en rik-rikare rikare och fattigare mekanism.
Tänk på detta eftersom det tros vara den allmänna förklaringen till "varför" Zipfs lag verkar med en sådan mystisk universalitet. Asteroidexemplet är ganska enkelt, men frågan är vad som händer över många repetitioner
Lite förvirrande?
Jo, jag gjorde ett gif för att köra den här första punkten hemma. OBS! diagrammet kommer att diskuteras senare, försök bara och visa experimentet.

Om vi observerar den faktiska månen visar det sig att, eftersom mängden asteroider ökar till stora mängder, observeras kraterdiametrarna så att de 20% av de största kratrarna närmar sig 80% av hela ytan.
Så när vi går till fler asteroider, närmar sig distributionen av populäraste till minst populära grupper en form av "ideal distribution" med denna 20/80 fastighet - en Pareto-distribution. Om du gör matte, visar det sig att (i allmänhet), om den största gruppen har storlek N, är den näst största gruppen runt storlek N / 2, den tredje N / 3 och så vidare och så vidare. Detta kallas Zipf's Law. Det konstiga är att Zipfs lag och Pareto-distribution fungerar för en förvirrande mängd element (asteroider) och grupper (kraterkluster). Naturligtvis finns det skews och slumpmässiga störningar, men den allmänna trenden är obestridlig.
Jag hoppas att du kan se hur asteroider som är mer benägna att slå stora kratrar på månen förbinder till att städerna blir mer attraktiva, om det redan finns fler människor som bor i dem. Men man måste inse att städer är långt ifrån de enda "grupper" som uppför sig enligt Zipf.
Här är några exempel från Mark Newmans forskning om Pareto-distributioner. OBS! Graferna är i loggskala som släpper ut den hyperboliska formen av kurvorna och presenterar ett nästan linjärt förhållande.
Initial y = aX ^ (- b)
Loggar på båda sidor => logg y = logga a - b logg X
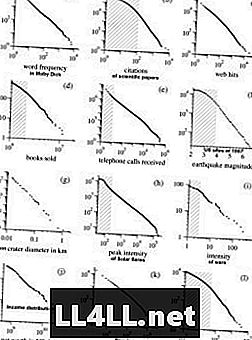
Intressant nog visar samma trend också av religiösa kulturer ... Den gemensamma egenskapen hos de flesta av dessa fenomen är helt enkelt denna "storgrupps-större" tendens. Så Zipfs lag är ihållande i mekanismer, där elementens preferenser är positivt kopplade till gruppens storlek (vilket betyder, ju större gruppen är desto mer sannolikt kommer den att växa). Därför tycker jag om att tänka på grupper som kluster och element som kluster.
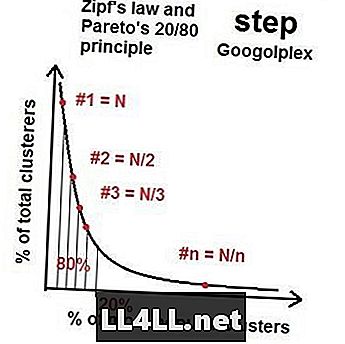
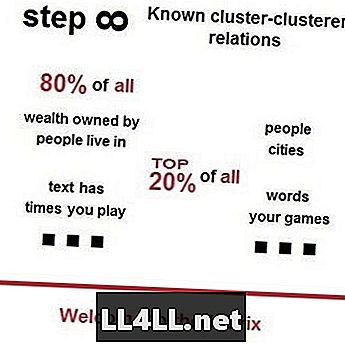
Zipfs lag på ångmarknaderna
Misstänker den sista? Här är hur lång tid folk spenderar på de mest populära spelen på Steam. Data från SteamSpy.
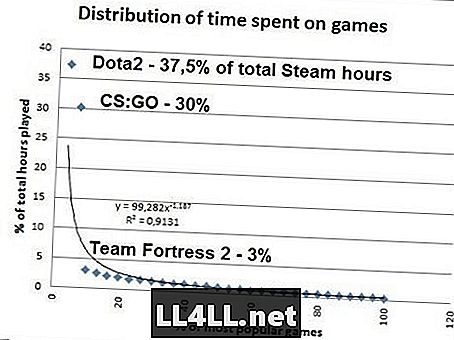
Om du gör matte, visar det sig att 20% av de mest populära Steam-spelen står för 80% av den totala leken, så Pareto 20/80-mysteriet fungerar som en charm här ... Man måste dock märka att Zipf att vara sant, CS: GO måste redovisa 37,5% / 2 = 18,8% av den totala tiden i stället för en hel del 30%. Men bortsett från denna outlier (STOPP SPELNING CS: GO) är den Zipf-liknande distributionen tydligt där.
Här är mängden kopior som säljs för de mest populära spelen.
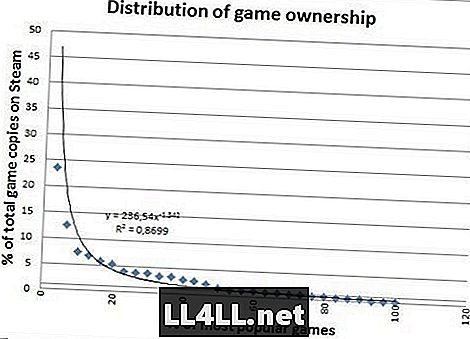
Ser mycket trevligare eh? Exemplar som säljs har inte stora utestängare så det passar väldigt bra, vilket är en anmärkningsvärd skillnad. Det finns emellertid något mer intressant att dra slutsatsen av skillnaderna i de två sista graferna.
Kan du märka hur "svansen" går till höger är lite fet i den andra grafen? Tja, i enkla termer säger det oss att de "relativt upopulära" spelen är faktiskt ganska mycket mer populära än i föregående plot.
Det visar sig faktiskt att 20% av de mest populära spelen står för endast 60% av försäljningen, mot 80% av spelningen. Intressant? Du satsar din röv det är.
Vad kan vi lära oss om Steam?
Jo, det faktum att spelet popularitet följer Pareto distribution berätta är att det verkligen finns någon form av positiv nätverkseffekt, vilket gör att spelare väljer spel som redan spelas av fler människor. Vad skillnaden i svans av svans berättar för oss är att Steam-användare är mycket mer "gruppstor-blind" när de köper spel än de är när de spelar dem.
Tänk på det - ju fler människor köper spel oavsett "den nuvarande populära opinionen", desto mer utplattad kommer Pareto-distributionen, eftersom det är mindre troligt att stora spel växer vidare. Om ingen gav en råttor rumpa om hur många som redan spelar ett spel och tillgängligheten av alla spel var densamma, så skulle vi förvänta oss att 20% av de mest populära spelen skulle stå för cirka 50% av försäljningen och lektiden (t.ex. normalt distribuerad).
Slutsatser
Så det finns två faktorer som bidrar till Pareto-distributionen på Steam-marknaderna - hur innovativa utvecklarna är (hur många nya månkratrar bildas) och hur mycket spelarna (asteroider) värderar den aktuella gruppstorleken när man väljer vilken grupp som ska gå med . Som det visar sig, spelare är mycket grupp-size-blind när man köper spel, men bara motsatsen när de spelar dem. Häftig va?
Om du vill lära dig mer om Zipfs lag- och energilagfördelningar, här är en trevlig föreläsning. Var noga med att ta en titt på Newmans papper!
Om du vill läsa mer av den här typen av saker kommer jag snart att försöka ansluta mig till denna observation till en modell, vilket visar att mer populära multiplayer-spel har högre priser (som länkar till spelarens preferens för att gå med i större grupper). Se artikeln här. Piece De Resistance-artikeln kommer att försöka ansluta sig till dessa teorier och förklara hur multiplayer-spel, sociala nätverk och städer i själva verket är alla anti-rivaliserande varor med nätverkseffekter (ju fler människor konsumerar en bra, ju mer varje enskild konsumentfördel) som har berättigade dem med denna zipfiska dimma av mysterium ...
Fram till dess - njut av er!
P.S. Pop i en kommentar med en rolig idé för en 20/80 relation du tror kan vara sant.
Mine är:
80% av folkens nostalgi orsakas av 20% av sina lyckligaste minnen (faktiskt bevisat för den takt som människor glömmer informationen på)
80% av massan är koncentrerad i 20% av de största rymdobjekten (faktiskt bevisad för fördelning av gravitationskraften)
Och naturligtvis
80% av röra i din toalett kommer från 20% av vad du äter (ingen akademisk forskning att tala om)